数的処理 方程式

840円を兄弟2人で分けるのに、兄は弟より340円多くもらうことにした。
弟は何円もらうか。
弟がもらう金額をX円とすると、兄のもらう金額は(x+340)円と表すことができる。
条件より x+x+340=840
これを解くと 2x+340=840
2x=500
x=250
よって 250円となる
ポイントは、兄のもらう金額を(x+340)円と表すこと
1280円を姉妹2人で分けるのに姉は妹の⅓もらうことにした。
妹は何円もらうか。
姉がもらう金額をx円とすると妹のもらう金額は(3x)円と表すことができる。
条件より x+3x=1280
これを解くと 4x=1280
x=320
妹のもらう金額は3x円より 3×320=960
よって 960円
姉のもらう金額を(⅓x)円でもよい
鉛筆5本と消しゴム3個の値段は合わせて475円である。
また、鉛筆3本の値段と消しゴム2個の値段は等しい。
消しゴム1個の値段はいくらか。
鉛筆1本の値段をx円、消しゴム1個の値段をy円とすると、
条件より 5x+3y=475...①
3x=2y...②
という式が成立する。
加減法による場合
②より3x-2y=0...②‘
①×3-②‘×3より 15x+9y=1425
―)15x-10y=0
19y=1425
y=75
よって 75円
A君とB君が同時に貯金を始めました。A君は毎月6千円ずつ貯金していたが、
ある時、6か月貯金をやめ、その後は、毎月7千円ずつ貯金を払い戻し続けた。
B君は毎月3千円ずつ貯金し、25か月後には2人の貯金額は等しくなった。
A君が最高額になったのは、貯金を始めてから何か月後か。
A君が6千円ずつ貯金していた期間をxか月間、7千円ずつ貯金を払い戻していた
期間をyか月間とすると、条件より
x+6+y=25...①
6x-7y=3×25..②
という式が成り立つ。
①よりy=19-x...①‘
①‘を②に代入して
6xー7(19-x)=3×25
6xー133+7x=75
13x=208
x=16
よって 16か月後
(表)
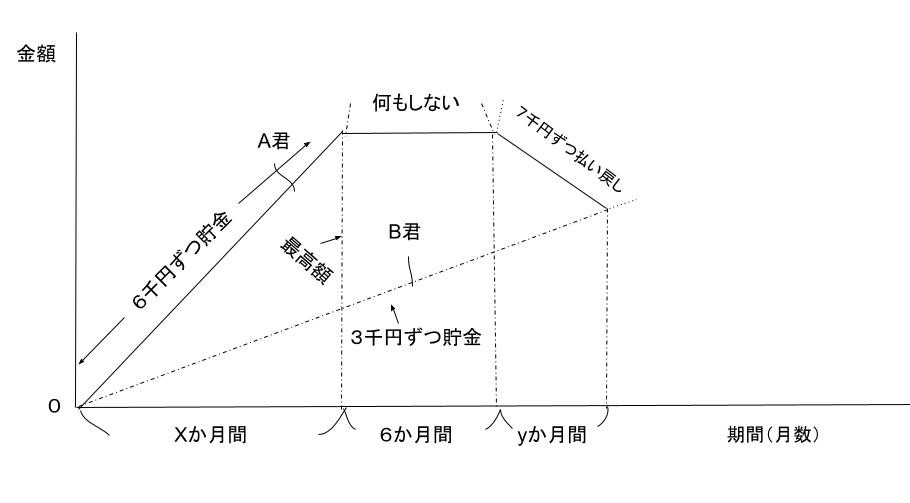
解説
まず、①は期間を式にしてます。
A君は、6千円貯金した期間をx期間とおき、
ある時、6か月間貯金をやめ、7千円ずつ払い戻した期間をyか月間
25か月間には貯金額が等しくなるため
x+6+y=25となる。
➁は6x-7yはA君の貯金ペース
6千円貯金した期間がx期間 6x
その後、7千円ずつ払い戻しした期間 ー7y
3×25はB君が毎月3か月間3千円ずつ貯金し
25か月後に2人の貯金額が等しくなった。
6x-7y=3×25となる。
考え方を分けていけば、難しくないのでしっかり落ち着いて解いていこう。